Interpretation

What problem this visualization solves

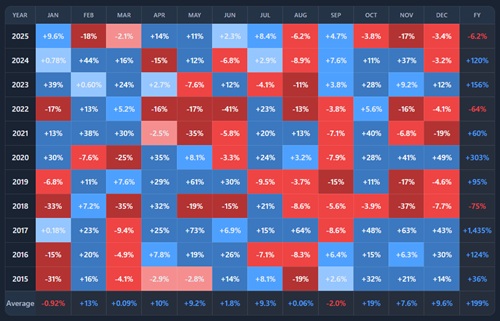
Seasonality claims are common in crypto — “May is weak”, “Q4 is bullish”, “September always dumps”, “Uptober” — but they are rarely tested across multiple years.

This visualization helps separate:

• recurring patterns
• one-off events
• narrative-driven hindsight

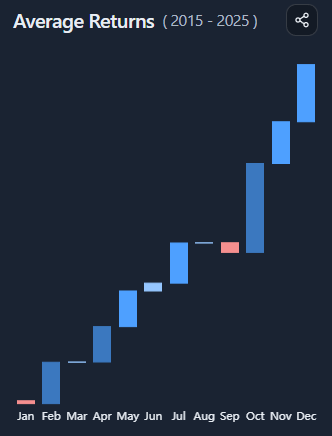
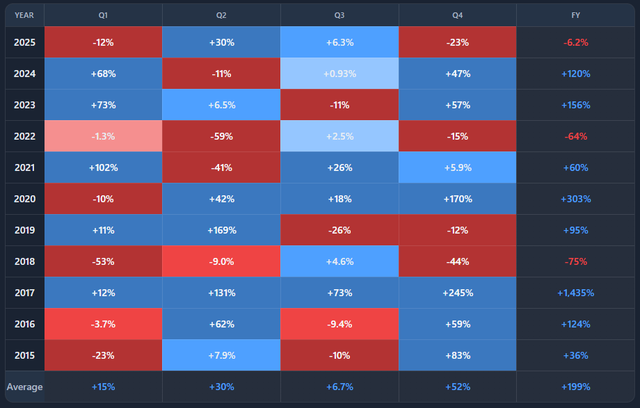
By showing returns by month or quarter across years, it makes it easier to see whether seasonality is persistent or anecdotal.

What you’re looking at

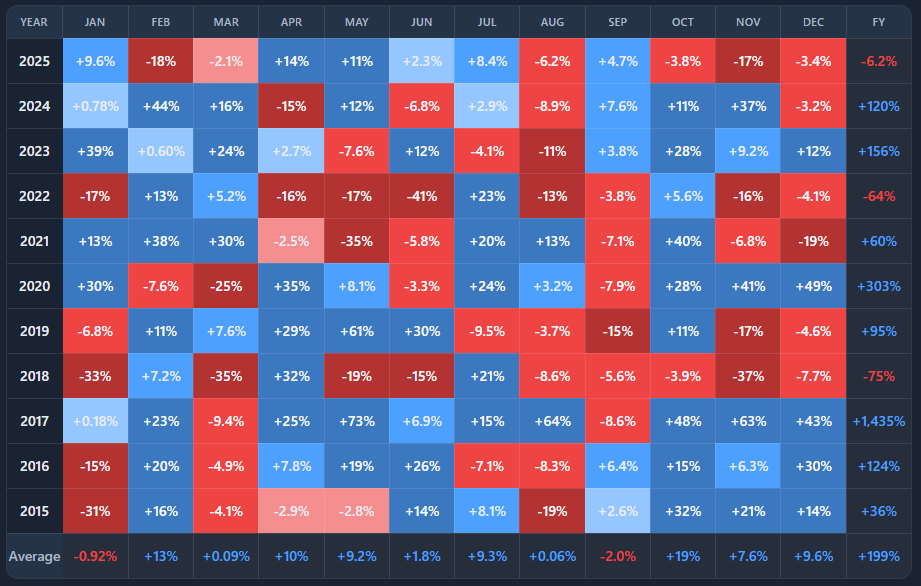
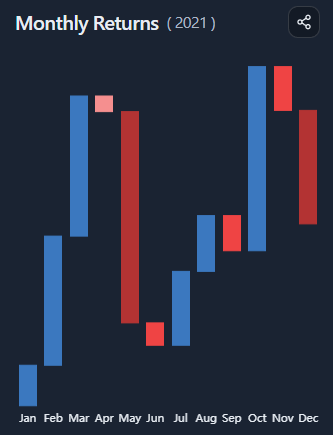
You are looking at a multi-year heatmap of returns, grouped by month or quarter.